Голая школьная математика

Волнующий вопрос о достоверности результатов выборов в Госдуму 4 декабря становится все менее актуальным – люди привыкают ко всему. Зато скоро станет сверхактуальным вопрос о президентских выборах 4 марта. Достоверность декабрьских результатов можно проверить иным способом, который пока не обсуждался широко, который прост и понятен, хотя не сможет, наверно, дать ответ на вопросы: КТО, КАК, КОГДА, ЗАЧЕМ и НАСКОЛЬКО вмешивался и корректировал результаты.

1. Немного почти школьной арифметики

Если представить себе колесо вроде рулетки, но с 10 цифрами, то нетрудно догадаться, что закрутив колесо 100 раз, мы получим примерно по 10 выпадений каждой цифры. «Примерно» – потому что, возможны случайные отклонения. Но, с другой стороны, если все 100 раз колесо остановится на цифре «3», вряд ли кто сочтет такой результат случайным совпадением. Граница между «случайностью» и «закономерностью» чуть ли не со времен Гаусса, то есть уже 200 лет, принимается равной некоей величине, которую называют «три сигма» — 3σ. Величину σ можно подсчитать по школьной формуле, это √(pqN). В нашем случае p=0,1 – вероятность выпадения одной определенной цифры из десяти, а q=0,9 – вероятность противоположного исхода, N – число испытаний, в нашем примере это 100. Тогда получится, что «3 сигма» равна 9. То есть результат для каждой цифры колеблется вокруг 10, с размахом 9, а значит от 1 до 19. Довольно «либерально», не правда ли? Но теория вероятностей утверждает, что в 99,7% случаев результат укладывается в этот диапазон. Можно и просто разделить число выпадений цифры на число опытов с рулеткой N и тогда мы должны ждать, что каждая цифра будет выпадать с частотой около 0,1 и с σ=√(pq/N)
Вот, что получится, если не 100, а сто тысяч раз закрутить рулетку с 10 цифрами.

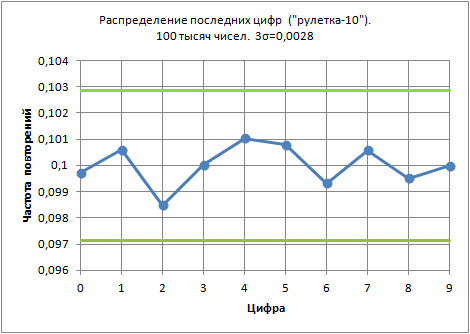
Зеленые линии как раз показывают плюс/минус три сигмы к средней величине 0,1 и видно, как все точки лежат внутри такого «зеленого коридора».
Но уж если результаты НЕ укладываются в коридор «три сигма», тогда произошло что-то существенное. Для физика-экспериментатора выход измеряемой величины за пределы «3 сигма» практически означает доказательство.
Но это лишь одна из десяти цифр. Чтобы учесть сразу все 10 цифр, используют величину, которую назвали «хи-квадрат» — χ2 или критерием Пирсона. Это сумма квадратов отклонений числа результатов по каждой цифре от ожидаемого. В нашем примере с сотней опытов эта разница от десяти, отнесенная к самому ожидаемому результату. Есть таблицы, которые показывают, что если в нашей рулетке χ2 стало равно 14,7, то такое может получиться в 10% случаев, ну а если достигло 27,9 – то это уже совсем неправдоподобно редко – лишь 0,1%.
Можно и сразу считать вероятность, с которой получается такое χ2, что мы и будем делать. Так если подсчитать χ2 для нашего графика, то она окажется равной 5,5, а вероятность составит 78%. Значит на графике результаты хорошей, честной рулетки.

2. А теперь займемся выборами.

Ведомство господина Чурова, повинуясь закону, сделало доступным результаты выборов по каждому из почти 100 тысяч избирательных участков России. Правда оно запрятало эти данные так глубоко, так тщательно разбило их на отдельные фрагменты, что рядовой и даже не рядовой пользователь интернета до них не доберется, а если и доберется, то только до отдельных фрагментов, которых без малого 100. А дальше придется или терпеливо собирать пазл, или просить помощи.
Но вот все трудности преодолены и у вас есть полная таблица с протоколами всех 95228 избирательных участков. В протоколах много граф. Выберем из них те, числа в которых, как правило, большие. Это число избирателей в списках; число избирателей получивших бюллетени в помещении для голосования; число бюллетеней, признанных действительными (то есть не испорченных), а также число голосов за каждую из двух самых больших партий. Всего у нас получится пять граф.
В каждом из этих 95228 чисел, в каждой из 5 граф будем смотреть лишь на ПОСЛЕДНЮЮ ЦИФРУ. Но и тут побеспокоимся – не будем брать в расчет однозначные и двузначные числа, только большие: трехзначные и четырехзначные: в них последняя цифра должна встречаться равновероятно, как в нашей мысленной рулетке с 10 ячейками.
Но сначала проделаем всё это для парламентских выборов 2010 года в Швеции. Просто для того, чтобы убедиться, что метод работает.

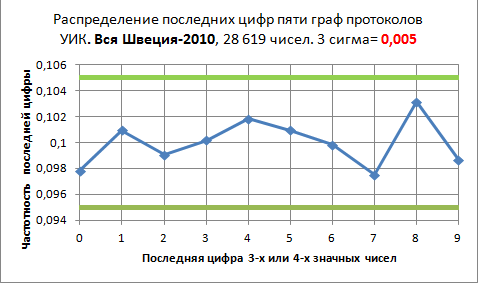
Ну что же – как и в нашей рулетке, здесь все точки пляшут внутри коридора, да и вероятность более 60%. Значит, и тут нет оснований сомневаться.
А теперь взглянем, используя тот же самый алгоритм и программу, на Российские выборы 4 декабря.

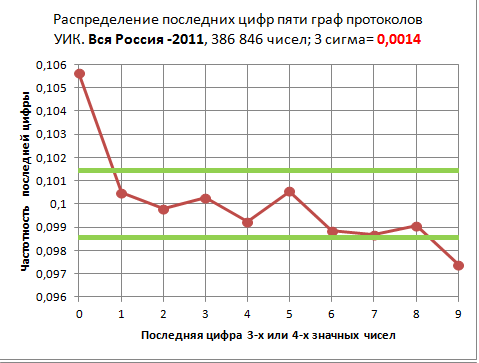
Разница не может не удивлять. На графике точки далеко вылезают из «зеленого коридора». Количество нулей среди последних цифр в России неправдоподобно велико, они встречаются много чаще, чем разрешает «три сигма». Да что там жалкие «три сигма», если такого не разрешают и 10 сигм! Вероятность, что такой результат получился совершенно случайно, описывается дробью, в знаменателе которой число большее, чем масса Земли в граммах (1027). А вот девятки встречаются почти столь же неправдоподобно редко. Даже семерки оказываются «нелюбимым» числом, всего лишь в 0,3% случаев такое может получиться случайно.
Но стоит лишь отодвинуть от подсчета голосов подчиненных господина Чурова («Россия без Ч»), то есть взять лишь те участки, где бюллетени считали не люди, а автоматы, то как по волшебству (или все же без «волшебства»?) всё становится почти таким же, как в Швеции (кстати, и число избирательных участков в этих случаях близкое: 4374 и 6063, и численность избирателей от 7 до 8 миллионов).

Почему «почти обыденным»? Да просто потому, что и в «Россию без Ч.» попадают числа избирателей в списках и числа выданных избирателям бюллетеней, а тут уж без людей не обошлось.
А если взять Дагестан, то там из 7176 чисел цифрой «0» заканчивается 1495 чисел, а вот цифрой «1» лишь 575, хотя число повторений каждой цифры с вероятностью 99,7% должно укладываться в диапазон от 642 до 794.

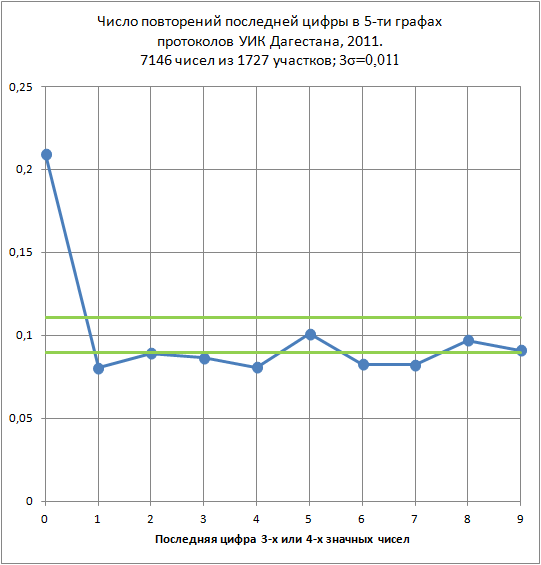
Разница уже не шесть, а 36 сигм! (Да и без всякой математики понятно, что если в нашей рулетке из 10 цифр сто раз из ста выпала одна и та же цифра, то рулетка явно мошенническая, а ведь тут разница лишь 11 сигма, а не 36). Только «5» пользуется некоторым преимуществом перед остальными цифрами, и лишь три из десяти цифр остаются в «зеленом коридоре». (Обратите внимание на то, что масштаб для Дагестана пришлось брать много мельче – иначе числа просто не умещаются)
Значения χ2 в Дагестане превосходят многие сотни, а мы помним, что уже значение χ2=28 дает вероятность, которую не встретишь на практике, менее 0,1%. Вероятность того, что такое распределение как на рисунке произошло в результате случайного стечения обстоятельств, равна дроби 1/10204, в знаменателе которой стоит число, много большее, чем число элементарных частиц во всей Вселенной (жалкие 1080!).
Результаты выборов на Кавказе на самом верху вертикали власти наивно объясняли особой тейповой структурой общества и уважением к старшим (начальству). Обществом, в котором все голосуют так, как сказал старейшина. Пусть так, поверим. Но, как мы видим, тогда придется объяснить, почему тейпы преимущественно состоят из целых десятков людей, которые так и живут десятками (лишь бы не по 7, или 9 или 11 человек), и на выборы ходят десятками, и партию выбирают десятками? Что это за чудеса? Может быть стоит объяснять это по-другому?
Читателю должно быть понятно, что таким способом можно заметить лишь самые грубые подделки, те, которые делаются без оглядки на возможные проверки, на какой-либо контроль, в твердой убежденности, что наверху «схавают» всё — лишь бы был приятный результат. Создается впечатление, что в некоторых местах выборов не было вообще, а результаты просто рисовали в протоколах, не утруждая себя даже и процедурами подсчета бюллетеней.

3. Регионы и тенденции

Точно такой же анализ можно сделать и по всем регионам России. У каждого получится свое значение вероятности: от совершенно неправдоподобной, как в Дагестане, до вполне разумной, как в Орловской области, где вычисленная по χ2 вероятность более 80%.
Теперь можно последовательно выключать из подсчетов результата голосования регионы, в которых вероятность, вычисленная по χ2,слишком мала, и смотреть на итоги. Ведь если преобладание нулей и недостаток единиц и девяток есть результат лишь маленького, простого и невинного округления, то на явке и результатах голосования это не должно сказаться, не правда ли?
Но проверим и это, и вот что тогда увидим.

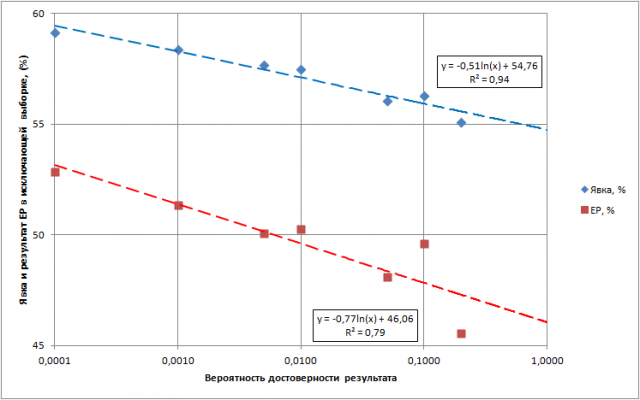
Здесь каждой точке соответствуют итоги голосования по всем регионам, в которых достоверность результатов не ниже указанной. Оказывается, что результат голосования все же зависит уровня достоверности, и при этом вполне отчетливо: чем выше достоверность, тем ниже явка и хуже результат одной из партий. Точки на левом краю графика дают явку и результат ЕР, представленный ЦИК. Но если последовательно отбрасывать наименее правдоподобные результаты, то значения упорно снижаются. При достоверности уже чуть большей, чем 1%, результат ЕР падает ниже 50%, при этом остается учтенным почти 39% всех активных избирателей. Остальные 60% с лишним (а значит мнение почти 40 миллионов граждан России) бессмысленно испорчены посторонним вмешательством.
Но если есть такая зависимость, то мы все же сможем ответить и на вопрос, который был задан в самом начале: «КТО, КАК, КОГДА, ЗАЧЕМ и НАСКОЛЬКО вмешивался и корректировал результаты».
КТО: региональные и местные власти. КАК: переписыванием или прямым «сочинением» результатов. КОГДА: при подготовке протоколов. ЗАЧЕМ: чтобы обеспечить цифры, которые понравятся «вертикали власти». НАСКОЛЬКО: настолько, чтобы вывести результат, нужный «вертикали», на требуемый ею уровень.

Вопросы вместо выводов

Есть три вопроса, которые нужно задать В.Чурову.

Почему такой, или более сложный анализ, не делает он и люди его ведомства?
Почему ЦИК не посылает строгие инспекции в регионы, в которых достоверность результатов падает до умопомрачительно малых величин?
Чем занят Центризбирком и его аппарат, которым именно за организацию честных выборов налогоплательщики платят немалые деньги?