Саратовский феномен (занимательная статистика)

Вероятно, большая часть читателей «Троицкого варианта — Наука» слышала о Саратовской аномалии. Примерно на 140 участках из 1885 доля голосов, поданных за «Единую Россию», лежит в диапазоне 62,1–62,3%. Этот феномен обнаружил Александр Киреев [1]. Люди, причастные к подсчету результатов в Саратовской области, назвали аномалию «математическим совпадением». Другие люди оценили вероятность этого «математического совпадения» — оценки колеблются от 10 -55 до 10-100, в зависимости от подхода. Мы же исходим из того, что из любого постыдного явления нашей жизни можно сделать интересный познавательный материал. Поэтому рассказываем о том, как оценить вероятность саратовского «математического совпадения» и как ее интерпретировать.
Вероятность статистического выброса зависит от так называемой нулевой гипотезы — как должно выглядеть истинное распределение без выброса. Допустим, у нас нет разумной нулевой гипотезы, и мы хотим поставить ограничение сверху: какова максимальная вероятность саратовского выброса при произвольных нулевых гипотезах, не противоречащих законам природы. Такую оценку сделал Борис Овчинников [2]. Для нее требуются два предположения:
- 62,2% — истинная доля избирателей Саратовской области, голосующих за «Единую Россию».
- Эти избиратели равномерно перемешаны по всем участкам и голосуют независимо друг от друга и от внешних факторов.
Тогда распределение голосов за «ЕР» на каждом участке будет с хорошей точностью гауссовским (более точно — биноминальным) со средним 62,2 и шириной, равной корню квадратному из числа проголосовавших за «ЕР» на участке (на самом деле участки разные, поэтому распределение будет суммой горбов разной ширины). У́же распределение быть в принципе не может, это азы математической статистики. Но и такой горб, близкий к гауссовскому, всё равно намного шире саратовского пика, и, по оценке Бориса Овчинникова, вероятность подобного выброса — 10-55. Казалось бы, на этом можно остановиться: верхняя оценка исчезающе мала, можно возбуждать уголовное дело о злостной фальсификации. Но мы, как принято у физиков, пойдем дальше и попробуем дать реалистичную оценку, пусть и не столь строго обоснованную.
На реальных выборах гауссовских распределений с дисперсией «корень из N» не бывает — они шире, из-за того что голосующие не независимы друг от друга (семьи, соседские компании) и от объективных внешних факторов (уровень жизни на участке, история района и т. п.). Мы можем попытаться позаимствовать нулевую гипотезу из жизни. Самое простое и самое естественное — взять результаты выборов в Саратовской области, вырезав из распределения пресловутый пик. Это будет наша нулевая гипотеза, а пик — статистический выброс, вероятность которого будем оценивать. «Но ведь и остальная часть кривой может быть сфальсифицирована», — скажет проницательный читатель. Конечно, но нулевая гипотеза как раз заключается в предположении о честности выборов.
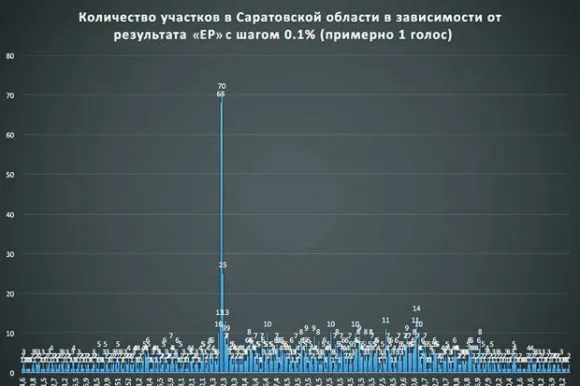
Реальное распределение возьмем из рис. 1, построенного Сергеем Романчуком. В два бина 62,1–62,3 попали 140 участков. По оценке Романчука, в близлежащих бинах в среднем по три участка, то есть под выбросом должно быть примерно 6 участков (лучшая точность нам не нужна ввиду абсурдности задачи). А наблюдаем 140. Вероятность выброса хорошо описывается распределением Пуассона (когда общее число участков много больше их числа в выбросе). Вот это распределение:
Здесь a – ожидаемое среднее, N — выпавшее число. При a = 6 и N = 140 имеем вероятность ~10-135 (Романчук, не пользуясь распределением Пуассона, получил «на пальцах» 10-100, что можно считать хорошим совпадением).
Что такое 10-135? Как представить значение подобного «математического совпадения»? Прибегнем к мысленному эксперименту. Чтобы с большой вероятностью произошло подобное совпадение, нужно сделать примерно 10135 равноценных испытаний. То есть провести именно столько выборов в миллионных регионах, разбитых на тысячу участков. На Земле их проводилось много, только в этих думских выборах участвовало 102 регионов (округляем до порядков). А по всему миру ежегодно проводятся десяток выборов, референдумов и голосований подобного масштаба (накидываем еще порядок). И так происходит большую часть XX века — примем за 100 лет. Беря числа с большим запасом, мы получим105 подобных голосований за всю земную историю. Не хватает 130 порядков величины.
Про очень большие числа, такие как, например, 1013, говорят «астрономическое число». Тогда 10135 — уже нечто гиперастрономическое. Перейдем на следующий, космологический масштаб. В наблюдаемой части Вселенной примерно 1012 галактик. В каждой из них 1011 звезд (берем с избытком). Итого 1023 звезд в наблюдаемой части Вселенной. Кстати, это больше, чем песчинок на всех пляжах Земли — примерно 10 тыс. км3 песка. Из них порядка 1022 звезд близки по своей светимости и массе к Солнцу. Из них, по данным телескопа «Кеплер», одна десятая, или примерно 1021, имеют планеты земного типа в зоне обитаемости. Предположим, что на всех таких планетах появляется жизнь и эволюционирует до разумных существ, дозревающих до демократии, требующей регулярных голосований. История земной демократии едва насчитывает 100 лет, но, может быть, цивилизации живут и проводят выборы очень долго — в среднем миллиард лет. Тогда за всю историю Вселенной в ее наблюдаемой части прошло 1021(планет) х 103 (в год) х 109(лет) = 1033 голосований, подобных по масштабу тому, что имело место в Саратовской области. Но нам нужно гораздо больше — не хватает еще 102 порядков!

Неужели такая вероятность физически не реализуема?
На самом деле не всё так плохо. Теория космологической инфляции гласит, что наблюдаемая область внутри горизонта — лишь микроскопическая часть от всей гигантской Вселенной, которая в свои первые мгновения росла по экспоненте, и где эта экспонента оборвалась — одному Богу известно. Она может быть и в 100 раз, и на 50 порядков больше размеров нашего горизонта. Если нам не хватает 102 порядков, то достаточно предположить, что размер Вселенной примерно на 34 порядка больше расстояния до горизонта (насколько расстояние до горизонта больше мелкой бактерии). И в такой Вселенной, плотно обжитой миллиардолетними цивилизациями, прилежно придерживающимися демократических процедур, с вероятностью порядка единицы за время ее существования где-то на выборах выпадет подобный результат. И эта честь досталась Саратовской области! А Элла Памфилова говорит, что этот факт не стоит и выеденного яйца. Ничего себе яйцо!
Борис Штерн