Некруглые монеты постоянного диаметра

В 2014 году британский Королевский монетный двор решил изменить дизайн монеты в 1 фунт. Причиной послужило то, что примерно 3% находившихся в обращении однофунтовых монет были фальшивыми — и это несмотря на ежегодное изъятие примерно двух миллионов подделок (в обращении находится полтора миллиарда однофунтовых монет). Утверждалось, что новый фунт будет самым защищенным от подделок среди всех известных монет. Как и на всех британских монетах, на аверсе должен изображаться профиль королевы (илл. 1); а вот на рисунок реверса был объявлен конкурс [1]. Выход монеты планировался в 2017 году.

1. Великобритания, проект монеты в 1 фунт, 2014 год (Royal Mint)

Дизайн монеты — правильный 12-угольник, который повторял дизайн традиционной трехпенсовой монеты 1937–1971 годов, — вызвал беспокойство у владельцев торговых автоматов, билетных касс и т. п.: ширина монеты зависела от того, под каким углом она попадает в приемник автомата, что могло создать сложности для автоматической оценки номинала и подлинности монеты. Поэтому в 2016 году углы были сглажены, стороны закруглены, и эксперименты показали, что такая монета с диаметром от 23,03 мм (между сторонами) до 23,43 мм (между углами) будет достаточно хорошо восприниматься торговыми автоматами. Монету выпустили 28 марта 2017 года; в течение полугода старые и новые фунты принимаются на равных, а 15 октября старые монеты выйдут из обращения. Автором изображения на реверсе, в котором объединены символы Англии, Шотландии, Уэльса и Северной Ирландии, стал пятнадцатилетний Дэвид Пирс, ученик гимназии королевы Марии в Уолсолле (илл. 2).

2. Великобритания, 1 фунт, 2017 год (Royal Mint)

На самом деле всех эти перипетий можно было избежать, и Королевский монетный двор знает как: с 1969 года Великобритания чеканит семиугольные пятидесятипенсовики постоянного диаметра, сначала 30 мм (илл. 3), а с 1998 года — 27,3 мм (илл. 4). Постоянство диаметра фигуры означает, что между любой парой параллельных касательных будет одно и то же расстояние. Стало быть, автомату всё равно, как в него засунут монету.

3. Великобритания, 50 пенсов, 1969 год (на аверсе профиль Елизаветы II второго типа, Арнольд Мачин)
(en.numista.com)

4. Великобритания, 50 пенсов, 2015 год (на аверсе профиль Елизаветы II пятого типа, Джоди Кларк)
(en.numista.com)

Аналогичные монеты чеканили территории, зависящие от Британской короны: Фолклендские острова, Гибралтар, Гернси, Остров Мэн, Джерси, — а также Ирландия (илл. 5). Семиугольными были и монеты в 20 пенсов (постоянный диаметр 21 мм), которые чеканятся с 1982 года (илл. 6).

5. Ирландия, 50 пингинов, 1977 год; диаметр 30 мм (en.numista.com)

6. Великобритания, 20 пенсов, 1997 год (на аверсе профиль Елизаветы II третьего типа, Ян Ранк-Бродли)
(en.numista.com)

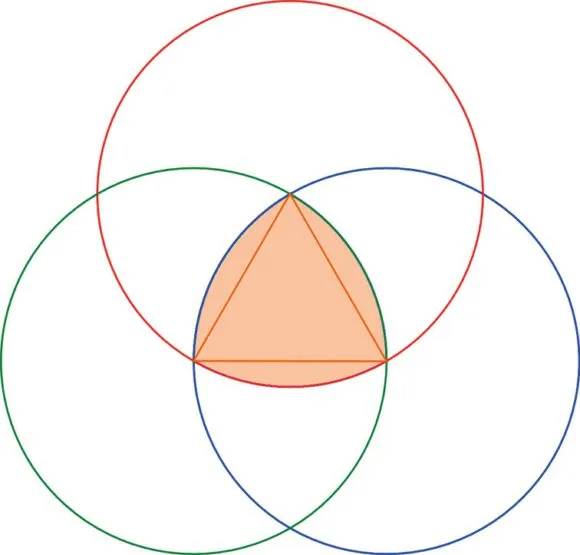
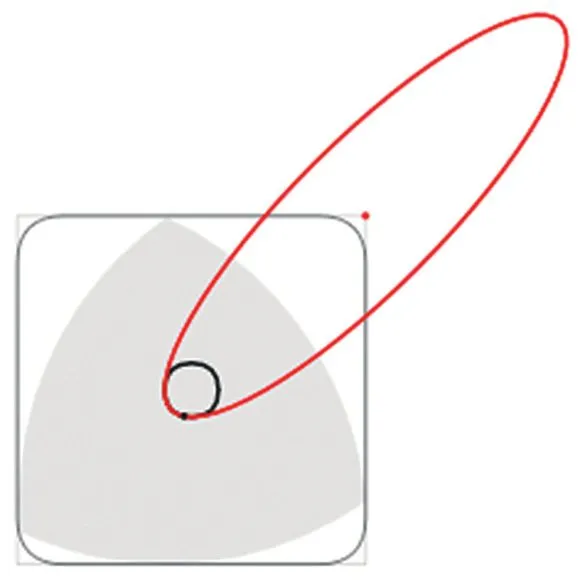
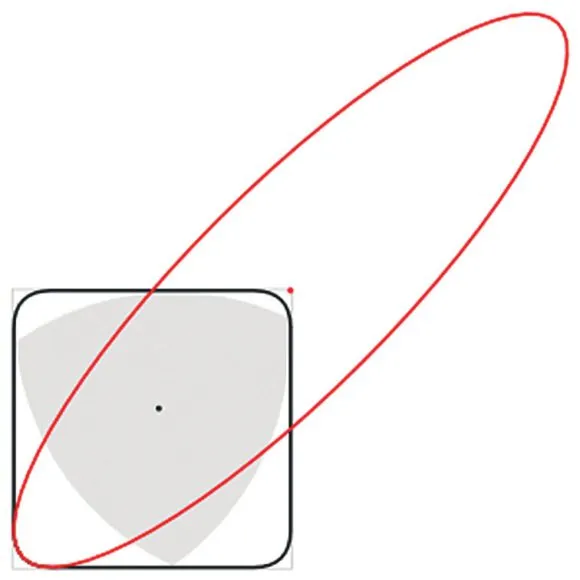
Все эти монеты имеют форму правильного многоугольника Рёло — фигуры постоянного диаметра, построенной на правильном многоугольнике. Геометрическое его построение несложно: надо провести дуги с центрами в вершинах и радиусами, равными по длине диагонали, которая ведет к вершинам, ограничивающим противоположное ребро. Монеты, перечисленные выше, имеют форму семиугольника Рёло; австрийские 5 евро (илл. 7) — девятиугольника, но самой известной фигурой является, конечно, треугольник Рёло (илл. 8). У него есть много замечательных свойств, например, можно вращать треугольник Рёло внутри квадрата так, что он всё время будет касаться всех четырех сторон квадрата [2]. При этом центр треугольника описывает фигуру, образованную четырьмя эллипсами (илл. 9), а сам треугольник заметает почти весь квадрат, кроме небольших областей в углах, также ограниченных эллипсами (илл. 10).

Форму треугольника Рёло имеют (разумеется) сувенирные монеты Бермуд (илл. 11 и 12) и памятная монета Канады (илл. 13). Для сравнения — просто треугольная австралийская монета памяти солдат Первой мировой войны (илл. 14).

11. Бермуды, 1 доллар, 1998 год — Бермудский треугольник (en.numista.com)

12. Бермуды, 9 долларов, 2007 год — крушение галеона «Сан-Педро» (Картахена — Кадис, ноябрь 1596 года); дата на монете не точна [3] (en.numista.com)

13. Канада, 50 центов, 2009 год (Royal Canadian Mint)

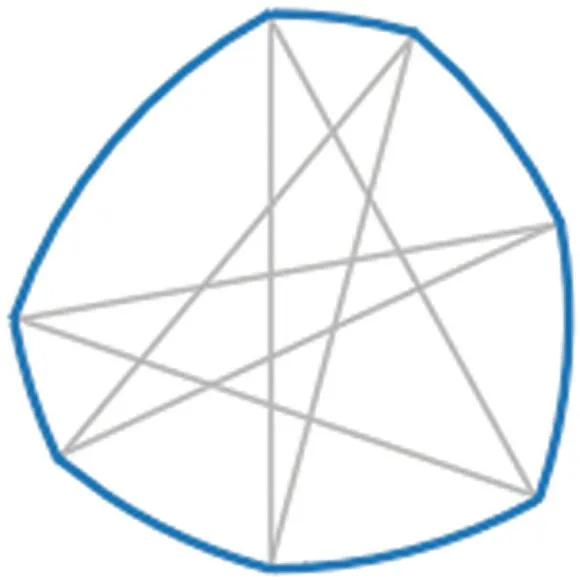
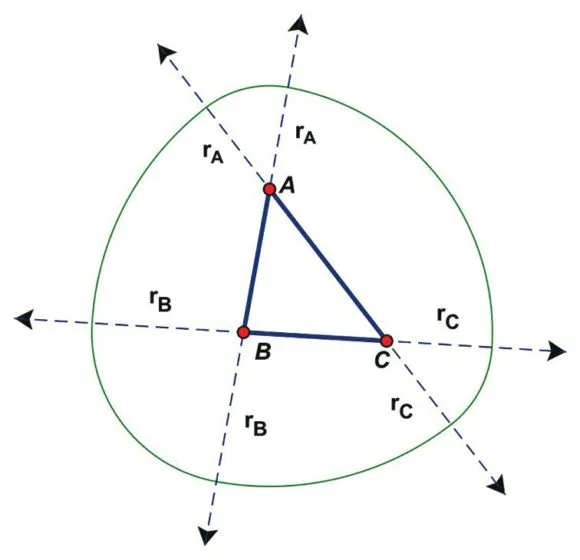
Существуют простые обобщения геометрической конструкции, с помощью которой получены эти монеты. Фигуру постоянного диаметра можно построить, взяв за основу звезду со сторонами одинаковой длины, не обязательно правильную (илл. 15). Можно также построить фигуру, начав с произвольного треугольника; при этом каждая вершина является центром не одной, а двух дуг, отчего углы получаются сглаженными (илл. 16) [4]. Пусть в треугольнике ABC угол А самый маленький (и, тем самым, противоположная сторона a самая короткая). Выберем неотрицательный радиус rA. Теперь нам нужно подобрать радиусы rВ и rС так, чтобы выполнялись соотношения a+rВ+rС=rA+b+rС=rA+rВ+c. Э т о несложно сделать, и диаметр фигуры получается равным 2rA+b+с–a. Самый маленький радиус регулирует сглаживание на углах: при rA=0 получаем фигуру с одним острым углом, а при rA→∞ фигура превращается в окружность. Существуют и другие конструкции (надо только, чтобы число вершин было нечетным), а также трехмерные обобщения, про которые рассказано, например, на канале YouTube “Numberphile” [5].

М. Г.