Гаусс против Чурова: промежуточный итог

- Аномалии в официальной статистике мартовских выборов подробно проанализировал Сергей Шпилькин в прошлом номере ТрВ-Наука [1]. О методологических основаниях их выявления и о значении этих аномалий для оценки результатов выборов рассуждает канд. биол. наук, доцент Департамента социологии Высшей школы экономики в Санкт-Петербурге Алексей Куприянов. Для интернет-версии статьи было добавлено три рисунка и пояснения к ним (см. ниже).
В связи с прошедшими выборами вновь оживились дискуссии об аномалиях в показателях электоральной статистики. В отличие от 2011–2012 годов, основной площадкой для обсуждения стал не «Живой Журнал», а «Фейсбук», однако некоторые темы оказались на удивление живучими. В частности, снова немало копий было сломано в ходе эпического противостояния «Гаусса» и «Чурова». Казалось бы, всё отспорено и решено, но до сих пор находятся как те, кто считает, что явка должна быть распределена нормально, так и те, кто полагает все оценки относительно фальсификации результатов выборов неверными на том основании, что явка вовсе не обязана следовать нормальному распределению. Благодаря упорству спорщиков мы еще долго не придем к согласию, но какой-то промежуточный итог подвести можно.
Почему распределение явки не должно быть нормальным?
Помимо социологических соображений о естественной пространственной сегрегации населения на это есть две чисто математические причины. Во-первых, область возможных значений явки — рациональные числа (т. е., числа, которые могут быть получены делением друг на друга целых чисел) в пределах от нуля до единицы, в то время как нормальное распределение непрерывно и бесконечно. Во-вторых, избирательные участки — это не случайные выборки из генеральной совокупности избирателей, и распределение средних показателей активности избирателей по ним (явок на участках) не может рассматриваться как случай, сводимый к Центральной предельной теореме1.
Распределение явок имело бы шансы приблизиться к нормальному, если бы участки формировали путем лотереи, проводимой среди всего населения страны (и несколько сотен счастливцев, вытянувших, скажем, номер 1768, где бы они ни жили, считались бы приписанными к участку с этим номером, точно так же как и вытянувшие остальные номера от 1 до 97 с лишним тысяч). Дело пошло бы еще лучше, если бы избиратели могли голосовать не целиком, а частями, отдавая, например, не 1, а любое случайное количество голоса от 0 до 1 (например, 0,967). Однако оба этих предложения довольно далеки от реальности.
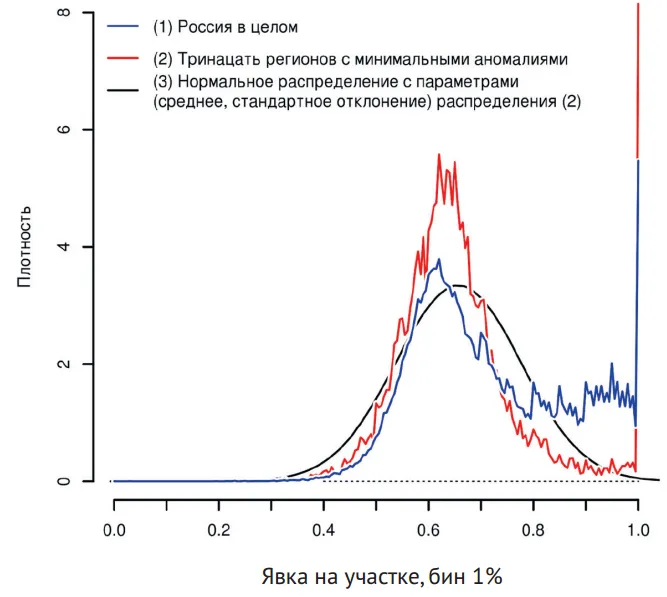
Кроме умозрительных соображений есть сравнительные данные по разным странам [2]. Ни в одной из них распределение явки по участкам не проходит стандартных тестов на нормальность. Не всякое распределение с колоколообразным графиком плотности можно признать нормальным в строгом математическом смысле. Требуется не просто «колокол», а «колокол» вполне определенных пропорций. Гистограмма явки обычно более островершинна, чем плотность нормального распределения с теми же математическим ожиданием и дисперсией, и несколько асимметрична.
Каким оно должно быть в России?
Мы не знаем наверняка. Имеющиеся искажения весьма значительны. Где-то истинные распределения не угадываются вообще (например, Чеченская или Кабардино-Балкарская республики), где-то видны только их следы (Татарстан, Кемеровская область). Вместе с тем у нас есть определенные теоретические соображения о том, как формируется распределение явки. Избиратели принимают решение об участии или неучастии в голосовании под влиянием множества факторов, модифицирующих даже самые стабильные паттерны электорального поведения.
В результате каждый регион характеризуется своими средними показателями активности избирателей с определенным разбросом значений на участках, связанным отчасти со случайными факторами. Практически в каждом крупном регионе распределение явок должно быть приблизительно колоколообразным, слегка асимметричным (обычно из-за несколько более высокой явки и большего разброса значений на небольших «сельских» участках, чем на более крупных «городских»), с низкими «плечами»/«хвостами».
Регионы могут отличаться друг от друга средними значениями явки или показателями разброса, однако эти различия должны формировать какой-то разумный географический паттерн: Север против Юга, Запад против Востока, город против сельских поселений. Очень помогает наличие исторических «внутренних» границ (например, части Польши, ранее входившие в состав Российской империи, Пруссии и Австрии, бывшие ГДР и ФРГ в составе объединенной Германии, Север и Юг Италии или США). Эти паттерны относительно стабильны во времени и не могут резко и разнонаправленно изменяться от одного электорального цикла к другому.
Россия велика и разнообразна, но естественная гетерогенность ее населения не может объяснить ни того уровня различий, который наблюдается в характере распределений явки в разных регионах (например, почти нулевой разброс в Кабардино-Балкарии, Ингушетии и Чечне в отдельные годы против вполне «человеческих» показателей Свердловской области, Карелии или Хакасии), ни географических странностей — непонятно, почему сходный характер распределений показывают отдаленные друг от друга Татарстан, Краснодарский край и Кемеровская область, между и рядом с которыми расположены почти «идеальные» в плане электоральных показателей регионы вроде Свердловской или Новосибирской областей. Гипотеза о естественной гетерогенности не позволяет объяснить и радикальные изменения характера распределения явки в Москве между выборами в Думу в 2011 году и президентскими в 2012 году.
Почему оно не может совпадать с «распределением Чурова»?
Потому что аномалии не сводятся к асимметрии распределения явок. Одна из важнейших особенностей «распределения Чурова» — аномальное тяготение к круглым числам. Начиная приблизительно с 80% явки (а в некоторые годы и с более низких значений) такие выбросы расположены на каждом целом процентном пункте. В совместной статье Дмитрия Кобака, Сергея Шпилькина и Максима Пшеничникова [3] был предложен алгоритм оценки вероятности формирования таких выбросов, основанный на симуляции распределения явки. Их алгоритм генерирует диапазон вероятных значений не для «истинного» распределения явки, которое было и остается неизвестным, а для «распределения Чурова», исходя из предположения, что резкая асимметрия его, возможно, соответствует реальности.
Анализ, вникнуть в логику которого и воспроизвести который может каждый желающий, показывает, что вероятность появления таких пиков в ходе естественных стохастических процессов ничтожно мала2. Этот метод, при всем его щадящем подходе к фальсификациям, достаточно чувствителен, чтобы зафиксировать аномальный характер явки даже в относительно «чистом» Петербурге (cм. рис. 1, 2). Этот метод позволяет надежно отличить естественные пики, обусловленные наличием «популярных» простых кратных отношений (1/2, 2/3, 3/4 и т.п.), от аномальных пиков, обусловленных «человеческим фактором».
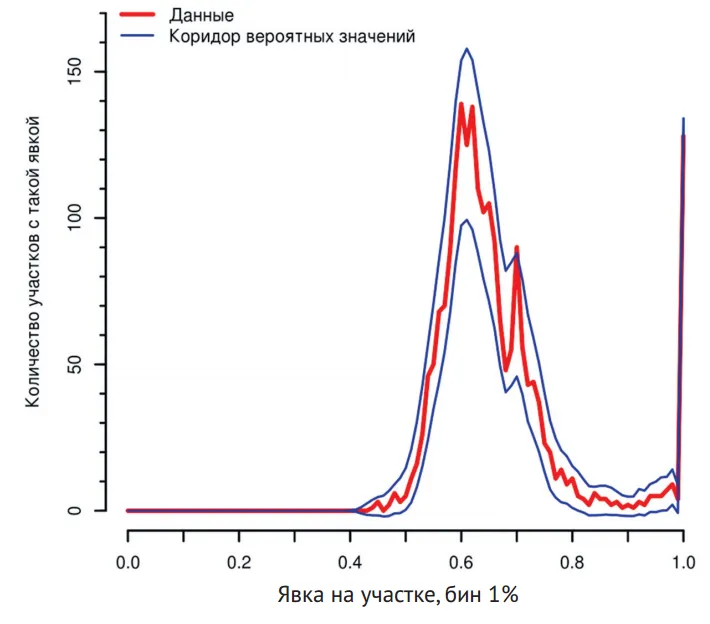
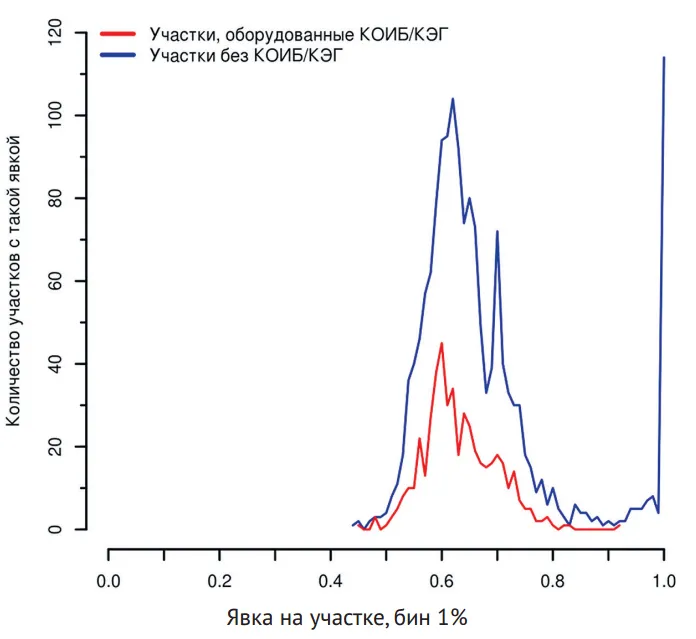
К круглым числам тяготеют и исходные абсолютные показатели (например, количество действительных бюллетеней). Анализ частот последних цифр также показывает статистически значимые отклонения от ожидаемого равномерного распределения [4, 5].
Доказывают ли аномалии в электоральной статистике наличие фальсификаций?
Да. В предыдущем разделе я постарался объяснить, почему для этого достаточно математических соображений. Однако у нас есть не только они. За прошедшие годы накопились сообщения наблюдателей о вбросах бюллетеней и грубых нарушениях на этапе подсчета голосов, о расхождениях между цифрами в полученных наблюдателями копиях протоколов и цифрами в ГАС «Выборы».
Eсть данные пересчета явки по официальным видеозаписям, значительно расходящиеся с данными, предоставленными участковыми комиссиями (рис. 3). В этом году работа c видеозаписями только началась, но уже первые результаты показывают на отдельных участках приписки в объеме от трети до двух третей голосов.
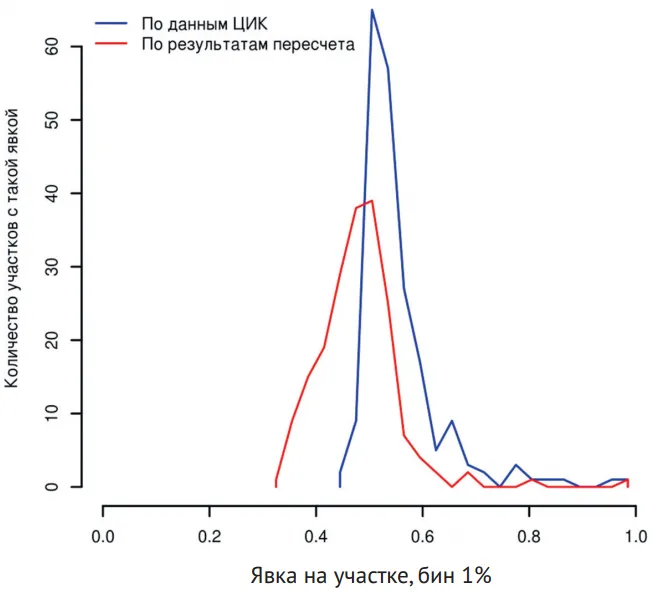
Все эти наблюдаемые манипуляции должны оставлять цифровые следы. Вбросы бюллетеней, «карусели» и подобные им технологии одновременно повышают явку и долю голосов за кандидата-бенефициара фальсификации, в результате чего облако точек на диаграмме рассеяния в осях явка/ доля голосов «размазывается» по дуге вверх и вправо, образуя хвост «кометы Чурова», сопровождающий ядро «честных» участков. Переброс голосов от одного кандидата к другому (без изменения явки) дает второе облако точек над основным ядром.
Согласованные действия фальсификаторов, ориентирующихся на определенный процент (часто некруглый) приводят к формированию полосовидных сгущений точек в неожиданных местах, вроде десятков участков с результатом «Единой России» в 62,2% на думских выборах в Саратове в 2016 году или 58% явки на губернаторских выборах в Петербурге в 2014-м.
Несогласованные действия тысяч фальсификаторов, ориентирующихся для простоты расчетов на целые или круглые проценты, приводят к формированию характерных пиков на целочисленных значениях в области высокой явки и высокой поддержки лидера (см. рис. 4). Они же отвечают и за избыточные частоты нулей в последних цифрах исходных показателей (например, числа действительных бюллетеней). Ту же природу имеет и «стена» в распределении явки на 50% в 2004 году, когда еще требовался кворум.
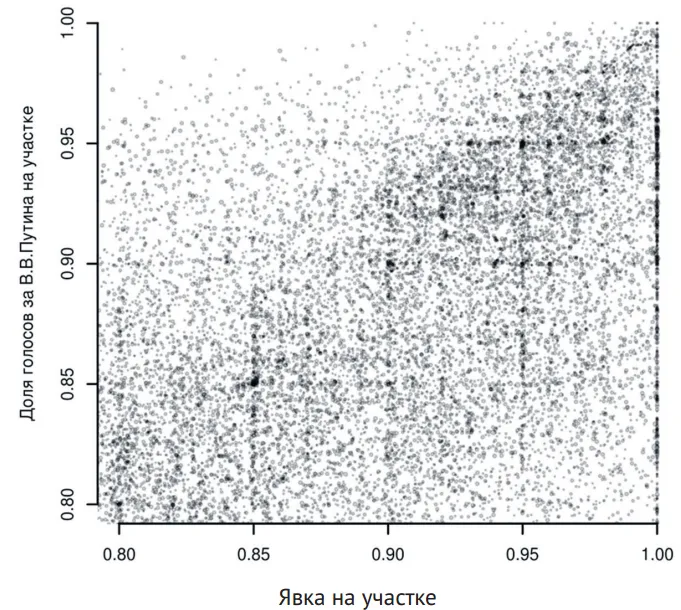
Осторожность требует говорить лишь о том, что наличие цифрового следа фальсификаций указывает на необходимость проверки. Однако проверки (например, пересчет явки по видео) только подтверждают наши осторожные подозрения. Сторонники альтернативных гипотез (пространственная сегрегация по социально-экономическим параметрам, совпадающая с границами избирательных участков, характер «мобилизации» избирателей в ходе избирательной кампании) пока не могут предъявить никаких сопоставимых по обоснованности результатов, которые помогли бы объяснить имеющийся масштаб аномалий.
Можно ли оценить масштабы фальсификаций и восстановить истинную картину явки?
Имеющиеся оценки носят приблизительный характер и, судя по всему, занижают масштаб фальсификаций. Связано это с тем, что в алгоритмы, на основе которых производятся вычисления, сознательно заложен ряд допущений «в пользу» фальсификаторов. Например, в модель Монте-Карло симуляции гистограммы явки, предложенной Кобаком, Пшеничниковым и Шпилькиным, заложено предположение о том, что явка на участках действительно такова, как в данных, предоставляемых ЦИК (что, как мы знаем, заведомо неверно).
Алгоритм для расчета превышения ожидаемой доли голосов тоньше — он отталкивается от того, что при «вбросе» бюллетеней одновременно с ростом явки должна расти доля только одного из кандидатов. При этом, во-первых, вынужденно не учитываются манипуляции в пользу других кандидатов (которые тоже иногда встречаются). Во-вторых, он нечувствителен к «перебросу» голосов от одного кандидата к другому. Наконец, не вполне ясно, насколько хорошо этот алгоритм работает в регионах с полностью или почти полностью нарисованными данными (в виду отсутствия базы для сравнения в виде пула «честных» участков), а таких регионов немало.
Неутомимый Сергей Шпилькин и другие энтузиасты обработали данные с детализацией до участков по всем президентским выборам начиная с 2000 года, пользуясь умеренной открытостью ЦИК. Если внимательно проанализировать эти данные, отсеивая все очевидные аномалии, остается всего несколько регионов с относительно стабильной репутацией: Алтайский край, Архангельская, Владимирская, Ивановская, Костромская, Магаданская, Мурманская, Сахалинская, Свердловская и Ярославская области, Ненецкий автономный округ, Республики Карелия и Хакасия.
Внимательный анализ показывает, что и они несвободны от аномалий (в частности, на выборах-2018 заметна незначительная аномалия явки в районе 70%), но на фоне других выглядят пристойно. (Есть еще около полутора десятков регионов, в которых в 2012 и 2018 годах аномалии носили весьма умеренный характер, например Москва; однако ситуация в предшествующие годы делает их непригодными для лонгитюдного (долгосрочного. — Ред.) анализа.)
Гистограмма явки, построенная по этим регионам, получается именно такой, как я описал выше: слегка асимметричной, с низкими «плечами», более островершинной, чем нормальное распределение с аналогичными параметрами (рис. 5). В ней даже есть пик на 100%. Есть основания полагать, что по России в целом всё должно выглядеть приблизительно так же.
Общее замечание о значении выявленных аномалий
Нередко приходится слышать, что выявляемые приписки не изменяют принципиально исход выборов или что они малы, поскольку доля участков, вносящих вклад, скажем, в аномальные пики на целых значениях процентов, ничтожна.
Мне представляется, что в обоих случаях это не так. Пики на правом «плече» распределения явки указывают не на точечные фальсификации на конкретных процентах, а на то, что, судя по всему, все в целом данные в области значений явки, превышающей 80%, не имеют почти никакого отношения к реальному волеизъявлению избирателей.
Наличие масштабных фальсификаций, охватывающих порой целые регионы, должно означать отмену результатов голосования на десятках тысяч участков, а возможно, и признание выборов в целом несостоявшимися. То, что этого не происходит, многое говорит нам о политической системе современной России.
Дополнительные материалы для Интернет-версии статьи.
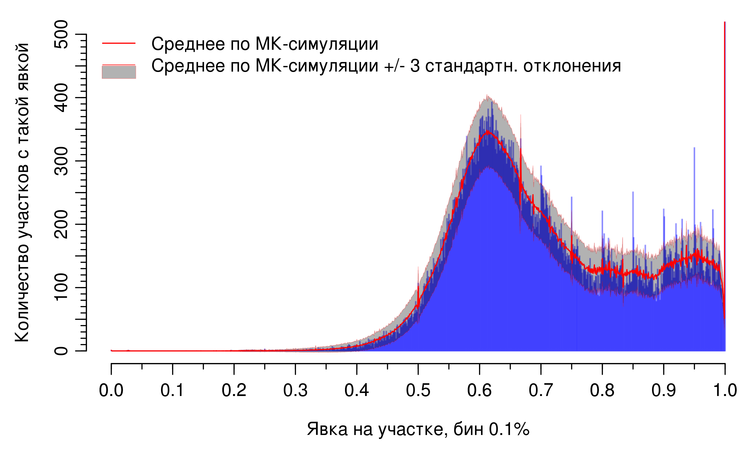
На этом рисунке представлены аномалии явки по России в целом во время президентских выборов 2018 года, гистограмма явки и коридор вероятных значений для гистограммы явки (среднее +/- 3 стандартных отклонения Монте-Карло симуляции). Обратите внимание на пики на кратных 5 и 10 процентах явки, выступающие далеко за пределы коридора и меньшего размера пики на каждом целом процентном пункте при явке выше 80%.
На этом графике (рис. 6) хорошо заметно отличие естественных пиков, связанных с часто встречающимися простыми кратными отношениями (например, 1/2 и 2/3, на 50% и 66,7% соответственно), и аномальными пиками. Над естественными пиками коридор вероятных значений так же образует узкий пик (включая участки со 100% явкой).
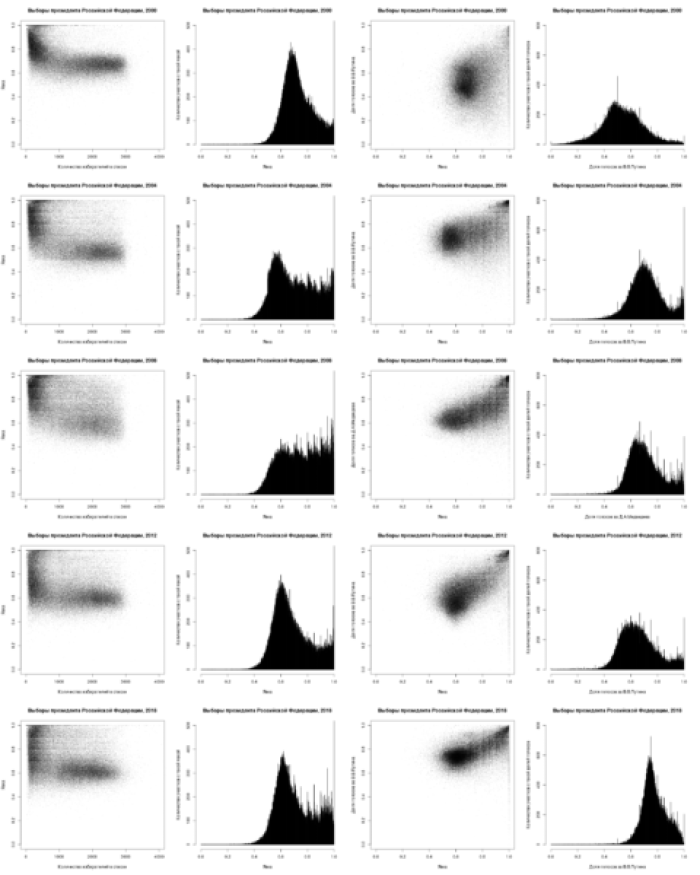
На Рис. 7 представлены диагностические графики для президентских выборов в России за 2000-2018 гг. Сверху — вниз: годы 2000, 2004, 2008, 2012, 2018. Слева — направо: диаграмма рассеяния в осях «количество зарегистрированных избирателей» / «явка на участке»; гистограмма явки на участках; диаграмма рассеяния в осях «явка на участке» / «доля голосов за лидера на участке»; гистограмма долей голосов за лидера на участке.
Обратите внимание на «волны» явки на «круглых» процентах, которые становятся заметны с 2004 году (в 2004 году особенно хорошо видна «волна» на отметке 50% — в этом году еще сохранялось требование о наличии квроума) и аналогичные «волны» доли голосов, отданных за лидера, наиболее заметные в 2008 году, но наблюдаемые с 2004 года. Заметно улучшение ситуации с явкой в 2012 году и ухудшение в 2018 году.
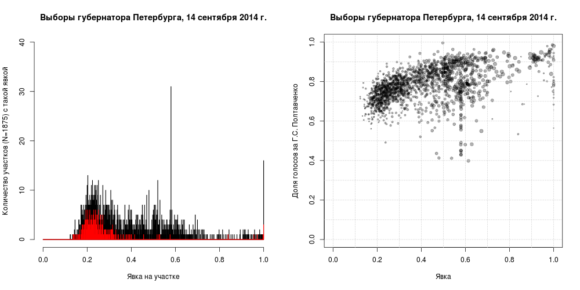
На рис. 8 представлены графики, отражающие аномалии явки на выбора губернатора Петербурга в 2014 году. Обратите внимание на вытянутое по дуге облако точек на диаграмме рассеяния справа и пик на 58% явки на обоих рисунках (31 участок с практически идентичными показателями явки). На гистограмме красным выделено распределение явок по участкам, подведомственным пяти территориальным избирательным комиссиям, в пределах которых не наблюдалось значительных аномалий (одно «ядро», нет «хвоста кометы»).
Благодарности
Я признателен Ефиму Галицкому [6], Роману Удоту и Дмитрию Рогозину за актуализацию дискуссий о форме распределения явки, Сергею Шпилькину за дополнительные пояснения по алгоритму симуляции, Борису Овчинникову [7] и Андрею Мятлеву за суммирование важных соображений в ходе дискуссии (их влияние заметно в этой заметке).
Алексей Куприянов
Графики построены автором на основе открытых данных.
1. Шпилькин Сергей. Выборы 2018 года: фактор X и «пила Чурова» // ТрВ–Наука № 252 от 24 апреля 2018.
2. Шалаев Н. Е. Распределение явки: норма и аномалии // Социодинамика. 2016. (7): 49–66.
3. Kobak D., S. Shpilkin, & Pshenichnikov M. S. Integer percentages as electoral falsification fingerprints // The Annals of Applied Statistics. 2016. 10(1). P. 54–73.
4. С. В. Голая школьная математика // ТрВ Онлайн, 28 февраля 2012.
5. С. В. Про арифметику и немножко про выборы // ТрВ Онлайн, 13 марта 2012.
6. Дискуссия, инициированная Ефимом Галицким.
7. Реплика Бориса Овчинникова.
1 Центральная предельная теорема — общее название ряда предельных теорем теории вероятностей, в которых устанавливается, что при большом числе слагаемых распределения сумм независимых случайных величин близки к нормальному распределению. — Ред. См.: Центральная предельная теорема // Большая российская энциклопедия.
2 Скрипт для обработки данных в среде R выложен на GitHub.